10.96. Kirby Monetary Choice Questionnaire (MCQ)¶
Series of hypothetical choices pitting an immediate amount of money against a delayed amount of money, to measure delay discounting.
10.96.1. History¶
Kirby et al. (1999) [27-item version].
Based on the earlier 21-item version: Kirby & Maraković (1996).
10.96.2. Source¶
From Kirby et al. (1999) as above.
10.96.3. Calculations¶
Hyperbolic delay discounting. The principle is to judge the value 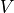 of two options,
of two options, 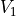 and
and 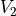 . Each has an amount
. Each has an amount 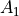 ,
,
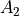 and a delay
and a delay 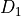 ,
, 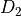 . Hyperbolic delay discounting
is assumed, according to the discounting parameter
. Hyperbolic delay discounting
is assumed, according to the discounting parameter 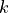 :
:
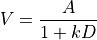
In the case of the Kirby MCQ, one option has zero delay (the small immediate
reward or SIR – call it option 1): 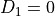 . One has a delay (the large
delayed reward or LDR – call it option 2).
. One has a delay (the large
delayed reward or LDR – call it option 2).
The values are therefore:
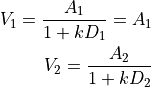
At indifference:
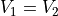
so at indifference:
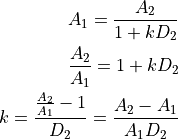
Given a set of trials, a subject’s indifference point 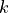 can be
calculated in various ways.
can be
calculated in various ways.
Kirby’s method (Kirby et al. 1999; Kirby, 2000). For each question, at
indifference,  can be calculated from the equations
above via
can be calculated from the equations
above via 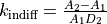 . Kirby’s method
compares subject’s choices against these indifference
. Kirby’s method
compares subject’s choices against these indifference 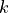 values: if the
subject chooses the delayed option, then
values: if the
subject chooses the delayed option, then 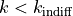 , and if
the subject chooses the immediate option, then
, and if
the subject chooses the immediate option, then 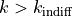 .
For a consistent series of choices, the geometric mean of the tested
.
For a consistent series of choices, the geometric mean of the tested 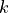 values straddling the subject’s indifference point is taken as the subject’s
values straddling the subject’s indifference point is taken as the subject’s
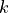 value. If the subject’s
value. If the subject’s 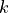 value falls outside the tested
range (i.e. all choices were for the immediate, or all for the delayed,
option), then the most extreme assessed
value falls outside the tested
range (i.e. all choices were for the immediate, or all for the delayed,
option), then the most extreme assessed 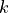 is used. Where choices are
not consistent, then the subject’s value of
is used. Where choices are
not consistent, then the subject’s value of 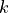 is taken as the
is taken as the 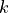 value with which the subject’s choices were most consistent (i.e. the most
choices were as predicted by that value of
value with which the subject’s choices were most consistent (i.e. the most
choices were as predicted by that value of 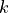 ) or, if there is no clear
winner, the geometric mean of multiple possible tested
) or, if there is no clear
winner, the geometric mean of multiple possible tested 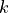 values that
were equally and maximally consistent with the subject’s choice. This geometric
mean approach reduces to the simple ‘consistent’ approach for consistent
choices, and thus may be used throughout.
values that
were equally and maximally consistent with the subject’s choice. This geometric
mean approach reduces to the simple ‘consistent’ approach for consistent
choices, and thus may be used throughout.
Wileyto et al.’s method (Wileyto et al., 2004). This method defines the
reward ratio 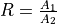 , and then predicts the probability
, and then predicts the probability
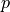 of choosing the delayed response using a logistic regression,
of choosing the delayed response using a logistic regression,
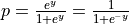 where
where 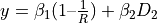 . That is,
. That is, 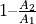 and
and 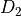 are used as predictors, obtaining the coefficients
are used as predictors, obtaining the coefficients
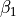 and
and 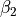 . At indifference, where
. At indifference, where 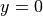 , this
gives
, this
gives 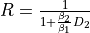 , and hence
, and hence 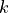 is estimated by
is estimated by 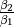 . However, it is possible for
such estimates to be negative under conditions of inconsistent choice.
. However, it is possible for
such estimates to be negative under conditions of inconsistent choice.
Todo
Reference RNC new method when published.
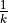 is the delay at which a prospective reward has decayed to
half its original value.
is the delay at which a prospective reward has decayed to
half its original value.
10.96.4. Intellectual property rights¶
Believed to contain no significant intellectual property, aside from the code, which is part of CamCOPS.
10.96.5. References¶
Kirby KN, Petry NM, Bickel WK (1999). Heroin addicts have higher discount rates for delayed rewards than non-drug-using controls. Journal of Experimental Psychology: General 128: 78-87. https://www.ncbi.nlm.nih.gov/pubmed/10100392
Kirby KN, Maraković NN (1996). Delay-discounting probabilistic rewards: Rates decrease as amounts increase. Psychon. Bull. Rev. 3: 100-104. https://www.ncbi.nlm.nih.gov/pubmed/24214810; https://doi.org/10.3758/BF03210748.
Kirby KN (2000) Instructions for inferring discount rates from choices between immediate and delayed rewards. Unpublished, Williams College.
Wileyto EP, Audrain-McGovern J, Epstein LH, Lerman C (2004). Using logistic regression to estimate delay-discounting functions. Behav Res Methods Instrum Comput J Psychon Soc Inc 36: 41–51. https://www.ncbi.nlm.nih.gov/pubmed/15190698.